反馈系统误差信号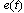 、 、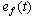 的稳态分量为系统的稳态误差,分别用 的稳态分量为系统的稳态误差,分别用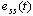 和 和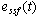 表示,简记为 表示,简记为 和 和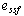 。 。
响应控制信号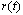 的稳态误差 的稳态误差 的计算 的计算
 终值定理法 本文来自www.eadianqi.com 终值定理法 本文来自www.eadianqi.com
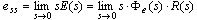
应用该方法时要求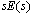 在右半平面解析。当 在右半平面解析。当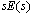 在坐标原点有极点时,从理论上讲不能使用该方法,但由于用该方法计算结果与实际相巧合,故仍可使用。 在坐标原点有极点时,从理论上讲不能使用该方法,但由于用该方法计算结果与实际相巧合,故仍可使用。
 静态误差系数法 静态误差系数法
设系统开环传递函数的一般形式为
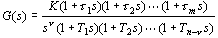 本文来自www.eadianqi.com 本文来自www.eadianqi.com
式中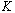 —开环增益, —开环增益, 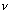 —系统型别。 —系统型别。
静态位置误差系数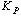 定义为 定义为
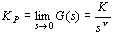
静态速度误差系数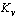 定义为 定义为
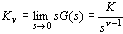 本文来自www.eadianqi.com 本文来自www.eadianqi.com
静态加速度误差系数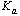 定义为 定义为
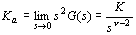
得单位反馈系统的稳态误差为
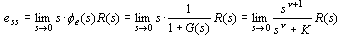
当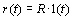 时,位置误差为 时,位置误差为
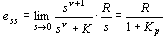 自动控制网www.eadianqi.com版权所有
当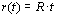 时,速度误差为 时,速度误差为
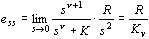
当 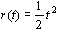 时,加速度误差为 时,加速度误差为
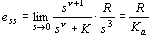
 自动控制网www.eadianqi.com版权所有
 动态误差系数法 动态误差系数法
利用前两种方法只局限于求出稳态误差的稳态值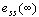 ,而利用动态误差系数法,可以研究输入信号几乎为任意时间函数时系统的稳态误差,且能反映稳态误差随时间的变化规律。 ,而利用动态误差系数法,可以研究输入信号几乎为任意时间函数时系统的稳态误差,且能反映稳态误差随时间的变化规律。
输入信号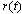 引起的稳态误差 引起的稳态误差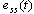 由下式给出 由下式给出
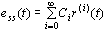
上式中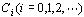 为动态误差系数,求法如下: 为动态误差系数,求法如下: 本文来自www.eadianqi.com
求导法 将系统误差传递函数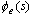 在 在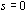 的临域内展开成泰勒级数,得 的临域内展开成泰勒级数,得
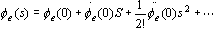
于是
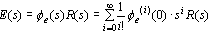
上式在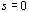 即 即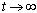 时成立,故在零初始条件下对上式取拉斯反变换得 本文来自www.eadianqi.com 时成立,故在零初始条件下对上式取拉斯反变换得 本文来自www.eadianqi.com
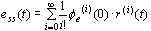
则
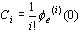 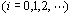
长除法 将误差传递函数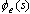 的分子多项式与分母多项式分别写成 的分子多项式与分母多项式分别写成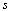 的升幂形式,然后利用长除法得到一个 的升幂形式,然后利用长除法得到一个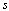 的升幂级数 的升幂级数 自动控制网www.eadianqi.com版权所有
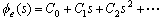
因而有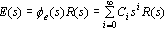 ,取拉斯反变换即得 ,取拉斯反变换即得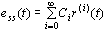 ,故式中 ,故式中 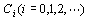 即为待求的动态误差系数。特别地,当 即为待求的动态误差系数。特别地,当 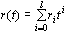 时 时 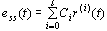 。 本文来自www.eadianqi.com 。 本文来自www.eadianqi.com
响应扰动信号 的稳态误差 的稳态误差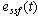 的计算 的计算
 终值定理法 终值定理法
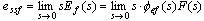
该方法要求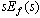 在 在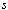 右半平面解析。 右半平面解析。 本文来自www.eadianqi.com
 动态误差系数法 动态误差系数法
由扰动信号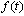 引起的稳态误差 引起的稳态误差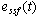 为 为
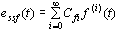
式中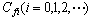 为扰动信号的动态误差系数,由求导法求得 为扰动信号的动态误差系数,由求导法求得
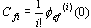 本文来自www.eadianqi.com 本文来自www.eadianqi.com
或由长除法求得 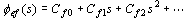
特别地,当 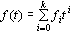 时, 时,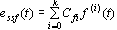 ,当控制信号 ,当控制信号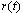 和扰动信号 和扰动信号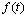 同时作用于系统时,系统的稳态误差为由 同时作用于系统时,系统的稳态误差为由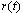 和 和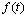 单独作用于系统时产生的稳态误差之和,这正是线性叠加原理的应用。 单独作用于系统时产生的稳态误差之和,这正是线性叠加原理的应用。 自动控制网www.eadianqi.com版权所有
|
