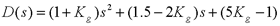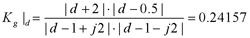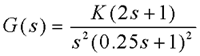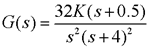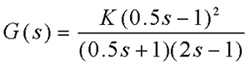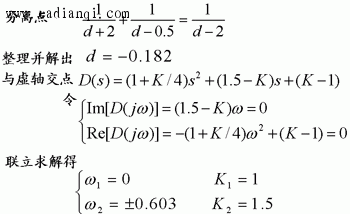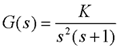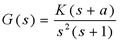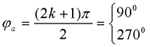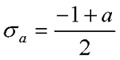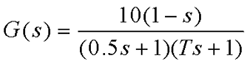|
闭环系统零、极点位置对时间响应性能的影响,可总结如下: 1、稳定性。 如果闭环极点全部位于s左半平面,则系统一定是稳定的,即稳定只与闭环极点位置有关,而与闭环零点位置无关。 2、运动形式。 如果闭环系统无零点,且闭环极点均为实数极点,则时间响应一定是单调的; 如果闭环极点均为复数极点,则时间响应一般是振荡的。 3、超调量。 超调量主要取决于闭环复数主导极点的衰减率
并与其它闭环零、极点接近坐标原点的程度有关。 本文来自www.eadianqi.com 5、实数零、极点影响。 零点减小系统阻尼,使峰值时间提前,超调量增大;极点增加系统阻尼,使峰值时间滞后,超调量减小。它们的作用,随着其本身接近坐标原点的程度而加强。 6、偶极子及其处理。 如果零、极点之间的距离比它们本身模值小一个数量级,则它们就构成了偶极子。远离原点的偶极子,其影响可略;接近原点的偶极子,其影响必须考虑。 7、主导极点。 在s平面上,最靠近虚轴而附近又无闭环零点的一些闭环极点,对系统性能影响最大,称为主导极点,凡比主导极点的实部大6倍以上的其他闭环零、极点,其影响均可忽略。 本文来自www.eadianqi.com
例题(1)
要求: 本文来自www.eadianqi.com
(2)由(1)中的计算结果可知,Kg稳定范围为0.2<kg<0.75
例2:单位负反馈系统的开环传递函数为 本文来自www.eadianqi.com
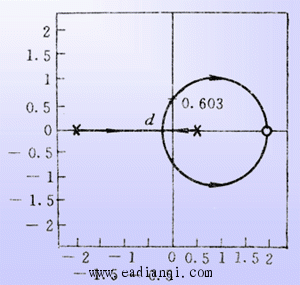
画出K从0->∞变化时闭环系统的根轨迹,并确定闭环系统稳定时的K值取值范围。 本文来自www.eadianqi.com
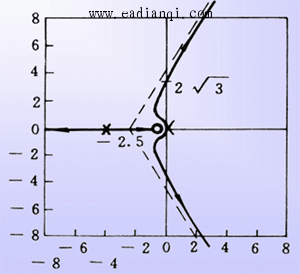
例3:已知单位反馈系统的开环传递函数为
例题(4) 本文来自www.eadianqi.com
该系统在K取任何正值时均不稳定,利用根轨迹图,说明在负实轴加一合适的开环零点-a可使系统稳定。
则渐进线与实轴的夹角 本文来自www.eadianqi.com
渐近线与实轴的交点 自动控制网www.eadianqi.com版权所有
由渐进线与实轴的交点可知,当a>1时,交点在s右半平面,系统仍不稳定。 本文来自www.eadianqi.com 例5 设单位反馈系统的开环传递函数为 自动控制网www.eadianqi.com版权所有
(1)画出T变化时闭环系统的根轨迹; |