|
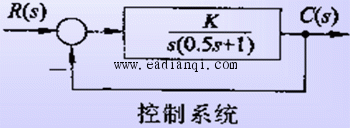
1、根轨迹概念 (1)、 根轨迹 开环系统(传递函数)的每一个参数从零变化到无穷大时,闭环系统特征方程根在 s平面上的轨迹称为根轨迹。
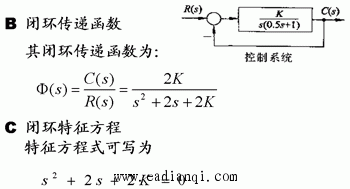
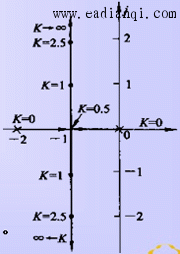
(2)、举例说明
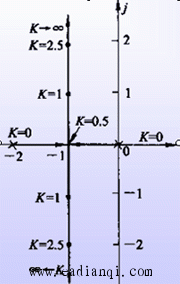
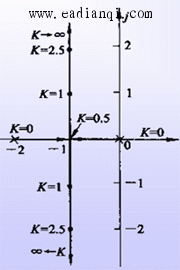
2 根轨迹与系统性能 (1)、稳定性 当开环增益从零变到无穷时,上面图中的根轨迹不会越过虚轴进入右半s平面,因此对所有的K值都是稳定的。
(2)、稳态性能 开环系统在坐标原点有一个极点,所以系统属I型系统,因而根轨迹上的K值就是静态速度误差系数。如果给定系统的稳态误差要求,则由根轨迹图可以确定闭环极点位置的容许范围。 (3)、动态性能 当0<K<0.5时,所有闭环极点位于实轴上,系统为过阻尼系统,单位阶跃响应为非周期过程; 当K=0.5时,闭环两个实数极点重合,系统为临界阻尼系统,单位阶跃响应仍为非周期过程,但响应速度较0<K <0.5情况为快; 当K>0.5时,闭环极为复数极点,系统为欠阻尼系统,单位阶跃响应为阻尼振荡过程,且超调量将随K值的增大而加大。
|