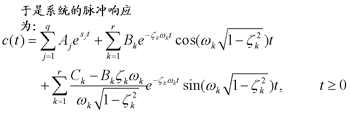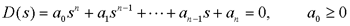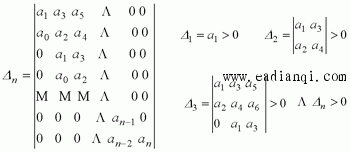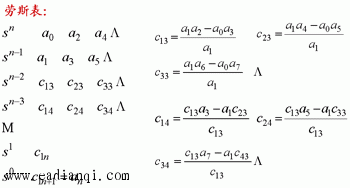|
1、稳定性的基本概念 (1)、表述一 若线性控制系统在初始扰动的影响下,其动态过程随时间的推移逐渐衰减并趋于零(原平衡工作点),则称系统渐进稳定,简称稳定;反之,若在初始扰动的影响下,系统的动态过程随时间的推移而发散,则称系统不稳定。 (2)、表述二
2、线性系统稳定的充要条件
通过分析上式可知,线性系统稳定的充分必要条件是:闭环系统特征方程的所有根均具有负实部;或者说,闭环传递函数的极点均严格位于左半s平面。 本文来自www.eadianqi.com
3、赫尔维茨稳定判据
则使线性系统稳定的必要条件是:在上式特征方程中,各项系数为正数。 自动控制网www.eadianqi.com版权所有
(2)、赫尔维茨稳定判据
(3)、李纳德-戚伯特稳定判据 在特征方程的所有系数为正的条件下,若所有奇次顺序赫尔维茨行列式亦必为正;反之亦然。这就是李纳德-戚帕特稳定判据。 (4)、举例说明 例:设某单位反馈系统的开环传递函数为
4、劳思稳定判据
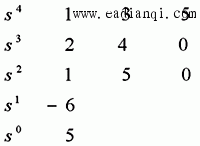
本文来自www.eadianqi.com 线性系统稳定的充要条件:劳斯表的第一列元素同号(或都大于零)。若第一列元素出现变号, 系统就不稳定,而且变号的次数,就表示特征方程的正实部根的数目。 例:设系统特征方程为 试用劳思稳定判据判别该系统的稳定性。 解:该系统的劳思表为
由于劳思表的第一列系数有两次变号,故系统不稳定,且有两个正实部根。 5、劳思判据的特殊情况 (1)、劳思表中某行的第一列项为零,而其余各项不为零,或不全为零,可以用(s+a)乘以原特征方程,其中a>0,再对新的特征方程应用劳思稳定判据。
(2)、劳思表中出现全零行 这种情况表明在特征方程中存在一些绝对值相同符号相反的特征根。此时可用全零行上面一行的系数构造一个辅助方程 ,并将辅助方程 对复变量 求导,用所得导数方程的系数取代全零行的元,便可按劳思稳定判据的要求继续运算下去。辅助方程的次数通常为偶数,它表明数值相同但符号相反的根数,所有那些数值相同但符号相异的根,均可由辅助方程求得。
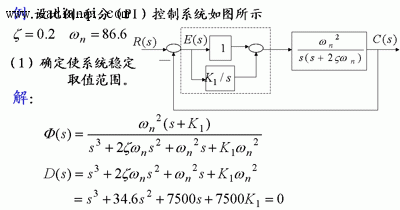
6 劳思稳定判据的应用
|